Le tri à bulles
Algorithmique > Algorithmes de tri > Tri à bulles [ Donner son avis ]Principe et fonctionnement
Le tri à bulles fait partie des tris simples à mettre en oeuvre mais peu performants. C'est un tri par sélection.Le principe général de fonctionnement est le suivant : on parcourt le tableau à trier à l'envers, en comparant les éléments consécutifs deux-à-deux tout en faisant ainsi "remonter" vers le début du tableau les éléments qui doivent être placés devant; à la manière d'une bulle ...
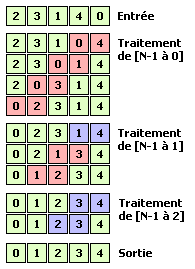 Lorsque l'on compare deux éléments : si ceux-ci sont dans le bon ordre, on les laisse dans le bon ordre [ opérations notées en bleu ] ;
s'ils ne sont pas dans le bon ordre, on les inverse [ opérations notées en rouge ].
Lorsque l'on compare deux éléments : si ceux-ci sont dans le bon ordre, on les laisse dans le bon ordre [ opérations notées en bleu ] ;
s'ils ne sont pas dans le bon ordre, on les inverse [ opérations notées en rouge ].Lorsque l'on a fini de parcourir le tableau une première fois, on est sûr d'avoir placé le premier élément à la bonne place. On parcourt donc de nouveau le tableau à l'envers pour placer le second élément, le troisième ... jusqu'au dernier.
Une optimisation classique du tri à bulles est présentée ici ; à savoir que lorsqu'à un stade donné, on a parcouru le tableau sans avoir à effectuer de permutations, c'est que celui-ci est trié. On peut donc arrêter le tri.
Complexité en temps et en mémoire
Au maximum, ce tri effectue n(n-1)/2 comparaisons, et en moyenne n(n-1)/4 permutations, ce qui en fait un tri quadratique. D'une façon générale et dans le pire des cas, le tri à bulles a donc une complexité en Ω(n²).Dans le meilleur des cas, on obtient cependant une complexité optimale de Ω(n). Il s'agit du cas où le tableau est déjà trié. Il est alors parcouru une et une seule fois et aucune permutation n'est effectuée.
Conditions d'utilisation
Le tri à bulles, bien qu' utilisable dans de nombreux cas et simple à implémenter est à éviter à cause de sa lenteur.Codes sources complets
-
Implémentation du tri à bulles (Code source en Pascal publié le 2006-11-01)
Implémentation standard du tri à bulles avec arrêt dès que la boucle principale n'a pas eu à permuter deux éléments.